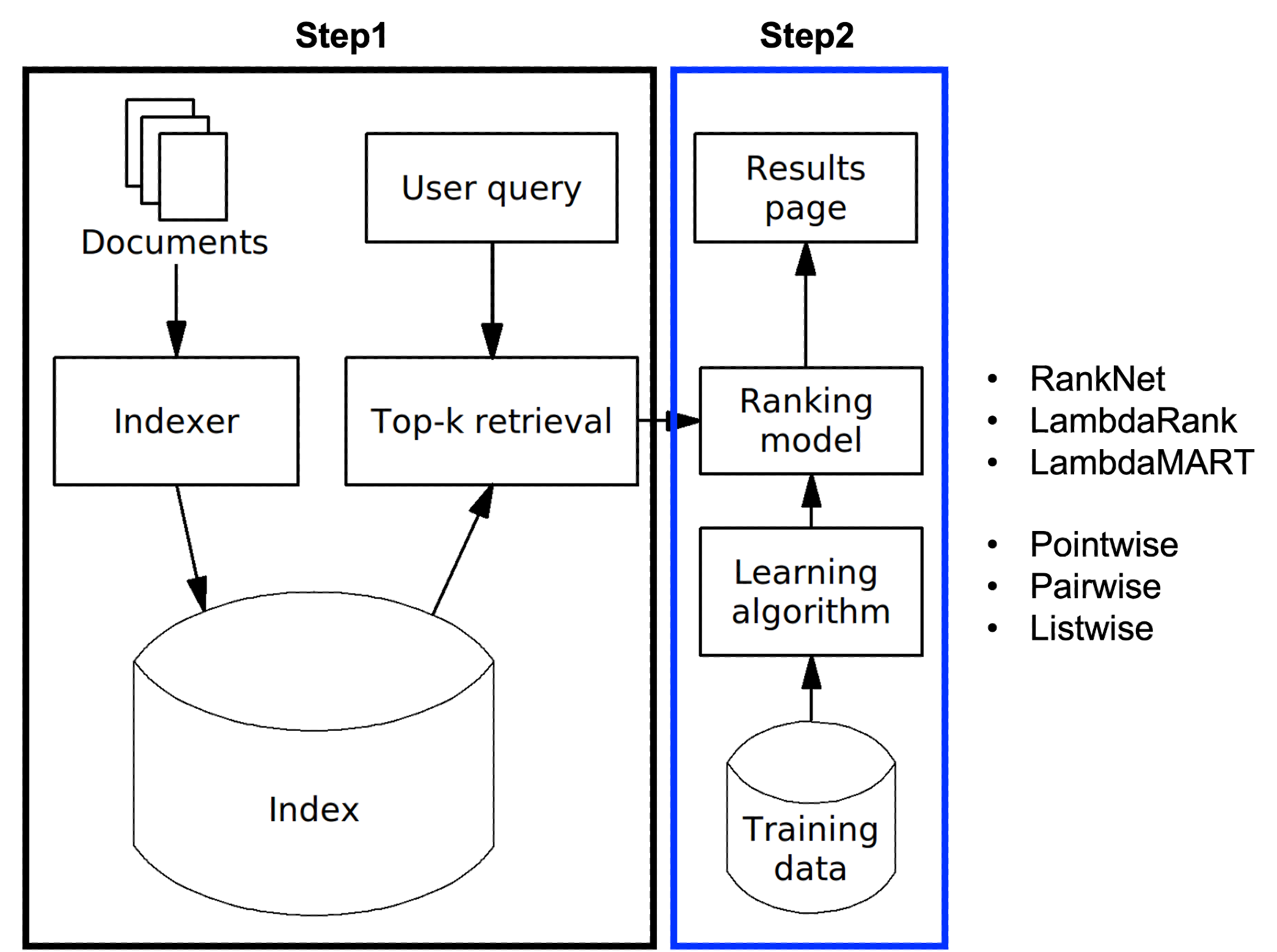
Multi-Armed Bandit

Recommender System

이번 포스팅은 추천시스템에서 많이 등장하는 Multi Armed Bandit(MAB)에 대한 내용이다. MAB 문제는 우리 일상에서도 흔히 찾아볼 수 있으며 여기에서는 bandit 문제에 대한 아이디어와, 이를 해결하는 간단한 알고리즘인 $\epsilon- $ greedy, Upper Confidence Bound, Tompson Sampling을 소개하도록 하겠다.

1. Motivation

Motivation idea

MAB 문제는 우리 일상에서 흔히 찾아볼 수 있으며, 우리는 알게 모르게 나름대로의 전략으로 여러 bandit 문제들을 풀어왔다. 이러한 bandit 문제는 time, reward, bandit, strategy 이라는 4가지의 요소로 구성되는데, 아래의 예시를 통해 구체적으로 살펴보자.

‘직장인 A의 점심시간 활용법’

직장인 A에게 1시간의 점심시간이 주어졌다. 만약 이 A가 유튜브를 보기로 결정했을 때, 어떤 영상을 얼만큼 봐야 최대의 즐거움을 느낄 수 있을까?

A는 주어진 1시간(time)동안 자신의 즐거움(reward)을 극대화시키기 위해 어떤 영상(bandit)을 선택할 것이고, 또 그 영상을 몇 분간 시청할 것(strategy) 이다. 조금 더 구체적으로 다음 예시를 살펴보자.

‘대학생 B의 기말고사 벼락치기’

내일이 시험인 대학생 B에게 공부할 수 있는 시간은 단 1일 뿐이다. 총 5개의 챕터가 시험범위라 할 때, 어떤 챕터를 먼저 어떻게 공부해야 최대로 높은 점수를 받을 수 있을까?

이 예시는 누구나 한번쯤은 겪어봤을 것이라 생각한다. 그간 우리는 1일(time) 동안 최대로 높은 점수(reward)를 받기 위해 5개의 챕터(bandit)를 어떤 식(strategy)으로 살펴봤는가? (참고로 필자는 가장 중요한 챕터 1개만 파는 스타일이다)

‘도박꾼 C의 슬롯머신’

도박꾼 C 앞에 10개의 슬롯머신이 있다. 총 3번의 기회가 있다고 할 때, 어떤 슬롯머신을 당겨야 최대의 보상을 얻을 수 있을까?

이 예시는 Multi Armed Bandit의 전형적인 문제로, 도박꾼은 3번의 기회(time) 동안 최대의 보상(reward)을 얻기 위해 10개의 슬롯머신(bandit)을 어떻게(strategy) 당겨야 할지 선택한다.

위 예시들은 우리가 일상에서 흔히 경험해본 것들이다. 정리하자면 Multi Armed Bandit은 time과 bandit(선택지)이 주어졌을 때, 어떤 선택 strategy(policy)을 구사해서 reward를 극대화 시키는 문제를 푸는 것이라 할 수 있다. Multi Arm이란 용어는 위 그림처럼, 팔이 여러 개인 도박꾼이 각 팔로 각 Bandit을 당기는 모습에서 유래했다.

Exploration(탐색)과 Exploitation(활용)의 Trade-Off

하지만 안타깝게도 우리의 시간과 비용은 한정적이기 때문에, 현실적으로 모든 bandit을 당겨보고 reward를 따져볼 수는 없다. 따라서 어떤 bandit을 선택해 얼마나 활용할지 결정해야 되는 문제에 직면하게 된다. 여기서 Exploration(탐색)과 Exploitation(활용)의 Trade-Off가 발생한다. 이 관점에서 위의 예시를 다시 살펴보자.

‘직장인 A의 Trade-Off’

현실적으로 직장인 A는 1시간 동안 모든 동영상을 다 볼 수는 없다. 따라서 동영상을 탐색(Exploration)해 하나를 결정 한 후, 얼마나 시청(Exploitation)할지 결정해야 된다. 만약 하나의 동영상만 시청할 경우(Exploitation만 하는 경우), 더 재밌는 동영상을 탐색할 기회를 잃게 된다. 반대로 어떤 동영상을 볼지 탐색만 할 경우(Exploration만 하는 경우), 결국 하나의 동영상도 제대로 보지 못하게 된다. 즉 우리는 우리도 모르게 탐색과 활용의 최적화를 하고 있는 것이다.

‘대학생 B의 Trade-Off’

대학생 B는 어떤 챕터를 먼저 공부할지 탐색(Exploration) 한 후, 해당 챕터를 얼마나 자세히 공부(Exploitation) 할지 결정해야 된다. 만약 하나의 챕터만 공부할 경우(Exploitation만 하는 경우) 다양한 챕터를 살펴보지 못한다. 반대로 다양한 챕터를 두루 볼 경우(Exploration만 하는 경우) 하나를 제대로 보지 못하는 문제가 있다. 이때 벼락치기를 최대한 효율적으로 하기 위해 어떻게 해야 할까? 이런 경험은 누구나 있을 것이므로 이 Trade-Off 가 쉽게 이해될 것이라 생각한다.

‘도박꾼 C의 Trade-Off’

도박꾼 C는 여러 개의 슬롯머신을 탐색(Exploration) 한 후, 몇 번 당길지(Exploitation) 결정해야 된다. 만약 하나의 슬롯머신만 당길 경우(Exploitation만 하는 경우), 더 큰 돈을 딸 수 있는 슬롯머신을 경험할 수 없다. 반대로 여러 슬롯머신을 당겨볼 경우(Exploration만 하는 경우) 돈을 딸 기회를 놓칠 수도 있다.

정리하자면 Exploration만 할 경우 bandit을 활용하지 못하고, Exploitation만 할 경우 다양한 bandit에 대한 정보를 얻을 수 없다. 따라서 최상의 reward를 얻기 위해서는 Exploration과 Exploitation의 최적화가 필요하며, 향후 소개할 알고리즘들은 이를 결정하는 방법들이 되겠다.

2. Multi Armed Bandit Problem

이제 본격적으로 Multi Armed Bandit 문제를 정의해보겠다. 앞서 bandit 문제는 time, bandit, reward, strategy 으로 구성된다고 하였으며, 이를 아래와 같이 표현하겠다. (strategy 는 4절에서 살펴본다.)

\[\begin{align*} \\ \bullet &\ \text{time :} \ \ t \ (t=1,2,...,N) \\ \bullet &\ \text{bandit :} \ \ b \ (b=1,2,...,k) \\ \bullet &\ \text{reward :} \ \ r_{t,b} \text{(reward of bandit $b$ at time $t$)} \\ \\ \end{align*}\]

일반적으로 최적화 문제를 풀 때, objective function을 정의한다. Multi Armed Bandit에서의 최적화 문제는 reward를 최대화 하는 것으로, regret이란 개념을 도입해 문제를 해결한다. regret이란 [optimal 선택에 의한 reward]와 [내 선택에 의한 reward]의 차이를 보여주는 지표로 아래와 같이 정의 된다.

\[\begin{align*} Regret &:= (\max_{b=1,2,...,k} E(\sum_{t=1}^{N}r_{t,b}))-E(\sum_{t=1}^{N} r_{t, b_{t}}) \\ &:= E(\sum_{t=1}^{N}(\mu_{t}^{*}-\mu_{t})) \\ \end{align*}\]

예를 들어 시점 $t$에 내가 bandit $b_{t}$를 선택했고, reward $r_{t, b_{t}}$를 얻었다고 하자. 그런데 만약 운이 나쁘게도 이때의 optimal bandit은 $b$였고, 그때의 reward가 $r_{t,b}$였다면 내 reward와 optimal reward 간의 차이가 발생할 것이다.

여기서 $\mu_{t}^{*}$가 시점 $t$의 optimal reward 평균, $\mu_{t}$가 시점 $t$의 내 reward 평균이라고 할 때, 우리의 목표는 이 차이의 평균을 최소화 하는 것이 되겠다. regret의 뜻이 ‘후회’라는 것을 고려해보면, 후회를 최소화 하는 것은 자연스럽다.

\[\begin{align*} \text{minimize}\ \ & Regret = E(\sum_{t=1}^{N}(\mu_{t}^{*}-\mu_{t})) \\ \end{align*}\]

지금까지 Multi Armed Bandit 문제의 목표를 수립했다. 아래에서는 이를 바탕으로 bandit을 선택하는 방법을 살펴보겠다.

3. Action-value function

벼락치기 전날 먼저 공부할 챕터를 정할 때, ‘시험 출제비율’이나 ‘공부량’ 등 저마다의 선택 기준이 존재한다. 마찬가지로, 매 시도 bandit을 선택할 때도 어떤 기준이 필요하다. 그리고 이런 기준은 앞서 설명했듯, regret을 최소화 시킬 수 있어야 한다. action-value function(행동가치함수) $Q$는 bandit을 선택하는 기준으로, 여기서는 다음과 같이 정의한다.

\[\begin{align*} \\ Q_{*}(b) &:= E(reward|bandit \ b) , \ \ b=1,2,...,k \\ \\ \end{align*}\]

즉 bandit $b$ 에 대한 행동가치함수는 $Q(b)$는 bandit $b$의 reward 평균이다. 우리는 매 시도 $Q$ 값이 가장 큰 bandit을 선택하게 되며, 이 값이 optimal에 가깝다고 가정한다. 아래는 $Q$를 보다 구체적으로 정의한 것이다.

\[\begin{align*} \\ Q_{t}(b) &= \frac{1}{N_{t-1}(b)}\sum_{i=1}^{t-1}R_{i}\ I(B_{i}=b), \ \ \ N_{t-1}(b) = \sum_{i=1}^{t-1}I(B_{i}=b) \\ &= \frac{1}{N_{t-1}(b)}(R_{t-1}\ I(B_{t-1}=b) + \sum_{i=1}^{t-2}R_{i}\ I(B_{i}=b)) \\ &= \frac{1}{N_{t-1}(b)}(R_{t-1}\ I(B_{t-1}=b) + N_{t-2}(b)Q_{t-1}(b)) \\ &= \frac{1}{N_{t-1}(b)}(R_{t-1}\ I(B_{t-1}=b) + (N_{t-1}(b)-1)Q_{t-1}(b)) \\ &= Q_{t-1}(b) + \frac{1}{N_{t-1}(b)}(R_{t-1}\ I(B_{t-1}=b) - Q_{t-1}(b)) \ \ \\ \\ \end{align*}\]

뭔가 복잡해 보이지만, 결국 $Q_{t}(b)$는 $t-1$ 시점 까지 bandit $b$의 reward 평균이란 뜻이다. 중요한 부분은 마지막 줄인데, $t$ 시점의 값인 $Q_{t}$를 업데이트 하기위해 이전 시점의 값인 $R_{t-1}$과 $Q_{t-1}$을 사용한다는 점이다. 이 부분은 아래에도 계속 등장하니 주의 깊게 살펴보길 바란다.

지금까지 bandit 선택 기준을 정의했다. 아래에서는 bandit을 탐색(Exploration)하고, 활용(Exploitation)하기 위한 몇 가지 streatgy를 살펴볼 것이다.

4. Bandit algorithm

이 절에서는 bandit을 탐색(Exploration)하고, 활용(Exploitation)하기 위한 streatgy 세가지를 살펴본다. 이 때 앞서 정의한 행동가치함수 $Q$를 사용하는 것에 주목하자.

$\epsilon$ - greedy

$\epsilon-$greedy는 아래와 같이 $\epsilon$의 확률로 탐색(Exploration)을 하고, 1-$\epsilon$ 의 확률로 활용(Exploitation)을 하는 전략이다. 구체적으로 시점 $t$에서 최적의 bandit $B(t)$를 결정한다고 할 때, 탐색은 $k$개의 bandit 중 1개를 랜덤으로 선택하는 것이며, 활용은 가장 큰 $Q$ 값을 갖는 bandit을 선택하는 것이다.

\[\begin{align*} B(t) \leftarrow \begin{cases} \text{argmax}_{b} Q_{t}(b),\ & \mbox{w.t} \ \ 1-\epsilon \\ \text{randomly chosen from} \ b & \mbox{w.t} \ \ \epsilon \end{cases} \end{align*}\]

보통 탐색과 활용을 결정할 때, 베르누이 분포에서 랜덤 확률변수를 발생시켜 결정한다. 즉 매 시도 $\text{action} \sim Ber(1, \epsilon)$로부터 action을 뽑아 그 값이 1이면 탐색을 하고, 0이면 활용을 하는 식이다.

Pseudo code

아래는 $\epsilon-$greedy의 수도 코드다. 주목해야할 부분은 4번 라인에서 $Q_{t}$가 업데이트 되는 방법이다. 3절에서 살펴본 식이 그대로 사용되고 있다.

이 알고리즘은 구현도 간단하고 단순하다. 하지만 최적의 bandit \(b^{*}\)를 찾았다 할지라도, $\epsilon$만큼 계속 탐색을 해야 되기 때문에 \(b^{*}\)에서 멀어질 수도 있다. 또 활용 과정에서 랜덤으로 bandit을 뽑기 때문에, 한번도 선택되지 않은 bandit이 있을 수도 있다.

Upper Confidence Bound

Upper Confidence Bound(UCB)는 불확실성이 큰(신뢰구간이 큰) bandit을 선택하는 전략이다. 예를 들어 어떤 슬롯머신이 10원이 나올 때도 있고, 10억이 나올 때도 있다면 이는 불확실성이 크다고 할 수 있을 것이다. UCB는 이러한 불확실성을 기준으로 선택을 하기 때문에, $\epsilon-$greedy와 달리 랜덤성이 없는 것이 특징이다.

일반적으로 통계학에서 불확실성은 신뢰구간으로 표현되는데, 아래는 정규분포의 모평균 $\mu$에 대한 신뢰구간이다.

\[\begin{align*} \hat{\mu}-z_{\alpha/2}\frac{\sigma}{\sqrt n}\ \ \leqq \ \ \mu \ \ \leqq \ \ \hat{\mu}+z_{\alpha/2}\frac{\sigma}{\sqrt n} \end{align*}\]

$\sigma$가 커질수록 이 upper bound가 커지는데, 이는 \(\hat{\mu}\)이 $\mu $를 제대로 추정하지 못한다는 것을 의미한다. 이러한 개념을 갖고, 아래 UCB가 어떻게 bandit을 선택하는지 살펴보자.

\[\begin{align*} B(t) \leftarrow \text{argmax}_{b}(Q_{t}(b) + c \sqrt\frac{\log(t)}{N_{t}(b)}) \end{align*}\]

위 식은 모평균 $ \mu $의 신뢰구간의 upper bound와 상당히 비슷하다. 여기서 $c$는 UCB 가중치로, 이 값이 0이면 $\epsilon-$greedy와 동일하다. $N_{t}$가 클수록 root 안의 값이 작아지기 때문에 UCB는 비교적 탐색이 덜 된 bandit을 선택하는 방법이라고 할 수 있다.

Pseudo code

UCB는 신뢰구간을 구해야 하므로, 처음에 모든 bandit을 한번씩 탐색하게 된다( 1~5라인). 이를 제외하면, 8번 라인 빼고는 $\epsilon-$greedy와 동일하다.

Tompson Sampling

$\epsilon-$greedy, UCB와 달리 Tompson Sampling(TS)은 $Q$에 대한 확률분포를 가정하여 이를 업데이트 한다. 위에서 자세히 설명하진 않았지만 보통 reward $R$은 다음과 같은 베르누이 분포로부터 발생 된다.

\[\begin{align*} \\ R(b) \sim Ber(1, p_{b}) \\ \end{align*}\]

$\epsilon-$greedy 와 UCB에서는 $p_{b}$를 임의로 설정한 반면, TS에서는 이를 추정한다. 중요한 것은 reward가 베르누이 분포를 따르므로, $p_{b} $가 reward의 평균인 $ Q(b)$와 동일하다는 것이다.

\[\begin{align*} \\ R(b) &\sim Ber(1, Q(b)), \ \ \because E(R(b)) = p_{b}=Q(b) \\ \end{align*} \\\]

우리의 목표가 최적의 bandit $B$를 찾아 $Q$를 업데이트 하는 것이라 할 때, TS에서 $Q$를 업데이트 하기 위해서는 물론 여러 방법이 있겠지만, 보통 베이즈 추정법을 사용한다. 이때 $Q$에 대한 사전 분포를 아래와 같이 베타분포로 가정한다.

\[\begin{align*} R(b)|Q(b) &\sim Ber(1, Q(b)), \ \ Q(b) \sim Beta(\alpha_{b}, \beta_{b}) \end{align*} \\\]

사전분포를 베타분포로 선택한 이유는 크게 2가지다. (1) 먼저 베타분포는 베르누이 분포의 conjugate prior다. 사후분포가 사전분포와 동일할 경우, 이런 사전 분포를 가르켜 conjugate prior라 한다. 특히 관심 함수가 베르누이 분포일 때, 사전분포를 베타분포로 선택하면 사후분포 역시 베타분포가 되기 때문에, 계산이 편리하고 해석이 용이해진다. (편의상 아래 식에서는 bandit notation을 생략)

\[\begin{align*} R|Q \sim~ & Ber(1,Q), \ \ Q \sim Beta(\alpha, \beta) \\ \\ f(Q|R) &= f(R|Q)f(Q) \\\\ &= \frac{Q^{R}(1-Q)^{1-R}\frac{1}{B(\alpha, \beta)} Q^{\alpha-1}(1-Q)^{\beta-1}}{\int_{0}^{1} f(R|Q)f(Q)dQ} \\ \\ &= \frac{Q^{\alpha+R-1}(1-Q)^{(\beta-R+1)-1}}{Beta(\alpha+R-1, \beta-R+1)} \ \ \sim Beta(\alpha+R, \ \beta-R+1) \\ \\ \end{align*} \\\]

위 결과 처럼 $Q$에 대한 사후분포 \(f(Q \vert R)\)는 \(f(Q)\)와 마찬가지로 베타분포를 따른다. 계산이 편리하다는 것은, 사후분포와 사전분포가 같은 파라미터 \(\alpha, \ \beta\)를 공유하기 때문이다. 또 사전, 사후 둘 다 동일한 분포를 따르기 때문에 분포의 변화를 쉽게 해석할 수 있다.

(2) 또 다른 이유는 베타 확률변수는 0과 1사이에서 정의되기 때문에 확률을 모델링 하기 적합하기 때문이다. 우리는 위에서 \(p=Q\)를 만족함을 살펴봤다. 따라서 $Q$는 확률과 동일하므로 0과 1사이에서 정의되어야 하며, 이런 분포로 베타분포가 적합하기 때문이다. 아래는 베타분포의 예시다.

\[\begin{align*} Q(=p) \sim Beta(\alpha, \beta) \end{align*}\]

Pseudo code

아래 수도코드는 각 bandit의 베타분포에서 샘플을 하나씩 뽑은 후(4번), 가장 큰 값을 갖는 bandit을 최적으로 선택한다(7번). 이를 $B(t)$라 할 때, $B(t)$의 reward 분포로 부터 $R(B(t))$를 발생시켜 파라미터를 업데이트 한다. 이때 이 값이 1이면 $ \alpha$를, 0이면 $\beta$를 업데이트 하는 것에 주목하자.

Tompson Sampling은 $Q$에 확률 분포를 가정함에 따라 굉장히 논리적인 구조를 갖고 있다. 여러 분야에서 많이 사용되는 알고리즘인 만큼, 그 흐름을 음미해보았으면 한다.

5. Tutorial

각 알고리즘에 대한 튜토리얼 코드는 여기를 참고 바란다.

Reference

https://fluruorubber.top/2020/01/14/Performance-of-Multi-armed-Bandit-Algorithms
https://yjjo.tistory.com/20?category=882868
https://brunch.co.kr/@chris-song/66