[논문 리뷰] From RankNet to LambdaRank to LambdaMART: An Overview - (1)

Recommender System

이번 포스팅은 Learning To Rank(LTR)에 관한 내용이다. LTR은 ‘랭킹 학습’ 문제로 주로 검색/추천 분야에서 사용된다. 이번 포스팅에서는 ‘추천에서의 랭킹 학습’이 무엇인지 자세히 살펴볼 것이며, 전반적인 내용 및 구성은 From RankNet to LambdaRank to LambdaMART: An Overview 논문을 참고하였다.

논문은 3개의 랭킹 모델(RankNet, LambdaRank, LambdaMART)이 각각 어떤 문제를 해결하며 발전해왔는지 보여준다. 특히 ‘Lambda’는 랭킹 문제의 코어를 이해하기 위해 반드시 알아야되는 개념이므로 비교적 깊이 생각해볼 것이다. 이번 포스팅은 시리즈로 구성하였고, LTR은 문제를 이해하는 것이 무엇보다 중요하므로 문제 정의부터 시작해볼 것이다. 이어 3가지 모델에 대해 순서대로 살펴보도록 하겠다.

1. Learning To Rank

위 그림은 Wikipedia의 Learning To Rank 아키텍쳐로, 설명을 위해 약간의 정보를 추가하였다. 그림을 보면 LTR은 크게 두 가지 문제로 이뤄진다. 유저에게 영화 아이템을 추천하는 문제를 가정해보자. 이때 Step1은 아래처럼 유저에게 후보 아이템을 추천해주는 단계다. 일반적으로 이미 만들어 둔 유저, 아이템 임베딩을 통해 후보군을 생성하곤 한다. Step2는 이렇게 얻어진 후보상품의 랭킹을 예측하는 과정이다. 정리하자면 LTR의 목표는 어떤 상품군의 랭킹을 예측하는 것이라 할 수 있겠다.

Rating prediction vs Ranking prediction

추천에는 여러 task가 있으며 가장 흔한 문제가 ‘평점 예측(rating prediction) 문제’다. 이는 유저가 아이템에 부여한 점수를 정확히 예측하는 것이 목표로, 이 점수가 가장 큰 순서대로 추천하게 된다. 반면 ‘랭킹 예측(ranking prediction) 문제’에서 정확한 점수 예측은 중요하지 않다. 여기서는 어떤 아이템을 더 선호하는지가 중요하며, 이 선호 관계를 학습하는 것이 목표다. 아래의 문제를 생각해보자.

예를 들어 어떤 유저가 {메트릭스: 5점, 타이타닉: 3점, 처키: 1점}을 부여했다고 하자. 어떤 문제를 정의하던 우리 추천시스템의 목표는 메트릭스와 비슷한 영화들을 먼저 추천하는 것이다. 이를 위해 ‘평점 문제’에서는 메트릭스의 평점 5점을 정확히 예측하고자 한다. 따라서 만약 우리가 제대로 문제를 풀었다면, 메트릭스가 다른 영화들보다 상대적으로 높게 예측될 것이다. 반면 ‘랭킹 문제’에서는 이 유저는 타이타닉 보다 메트릭스를, 처키보다 메트릭스를 ‘더’ 선호한다는 정보를 학습한다. 마찬가지로 제대로 문제를 풀었다면 로맨스나 공포보다는 액션영화가 먼저 추천될 것이다.

결과적으로 두 문제 모두 메트릭스를 먼저 추천한다. 하지만 그 기저에 이용하는 정보에는 차이가 있다. ‘평점 문제’에서는 ‘메트릭스의 점수가 5점’ 이라는 정보를, ‘랭킹 문제’에서는 ‘메트릭스를 더 선호’ 한다는 정보를 활용하는 것이다. 이것이 두 문제의 가장 큰 차이라고 할 수 있다.

2. Learning To Rank Dataset

지금까지 LTR의 문제를 정의하고, 이것이 평점 예측 문제와 어떤 차이가 있는지 살펴봤다. 이번 챕터에서는 LTR 데이터셋이 어떻게 구성되어 있는지 살펴볼 것이다. 이 부분을 굳이 다루는 이유는 평점 예측 문제를 떠올릴 때 머릿속에 유저-아이템 행렬을 그리는 것 처럼, LTR도 비슷한 컨셉을 잡아보기 위해서다. 아래 그림은 LTR 데이터셋의 기본 형태다.

일반적으로 검색분야에서 랭킹 문제는 검색어(query)와 관련된 문서(document)의 순서를 최적화하는 것이다. 따라서 데이터셋은 크게 3가지(검색어 별 문서, 검색어와 문서의 관계를 표현한 피처, 검색어와 문서의 관련성을 표현한 라벨) 정보로 구성된다. 예를 들어 검색어 q1과 관련된 문서는 {d6, d3}이고, (q1, d6)와 (q1, d3)의 관계를 표현한 피처가 각각 x1, x2다. 중요한 것은 relevance인데, 이는 각 문서가 검색어와 얼마나 관련성 있는지 나타내는 값으로, 이 정답을 어떻게 표현할지는 모델 개발자의 몫이다. 이제 이런 정보를 바탕으로, 검색 분야의 실제 벤치마크 데이터셋인 Microsoft Learning to Rank Datasets을 살펴보겠다.

마찬가지로 크게 3가지 정보로 구성되어 있지만, 이 데이터셋은 문서 정보가 따로 없고 각 행이 (query, document)셋을 나타낸다. 또한 피처같은 경우 총 136차원으로, 각 차원별 값을 dimension:value 형식으로 표현하고 있다.

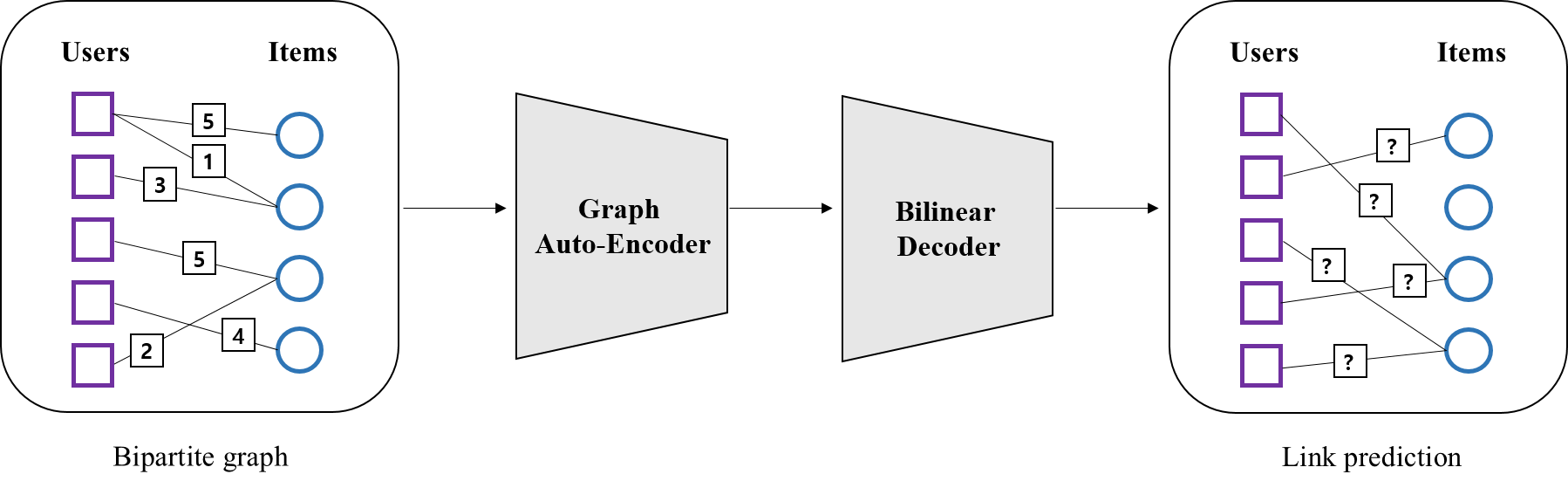
그렇다면 추천에서는 랭킹 학습을 위한 데이터셋을 어떻게 구성해야할까? 이를 위해 먼저 추천에서 어떤 랭킹 문제를 푸는지, 또 이를 바탕으로 query, document를 어떻게 정의할지 고민해봐야한다. 예를 들어 유저에게 영화를 추천해주는 상황을 가정해보자. 만약 우리가 아래 왼쪽 처럼 유저-아이템 평점 행렬을 만들 수 있다면, 랭킹학습을 위한 데이터셋을 쉽게 만들어 볼 수 있다.

여기서 유저는 검색어, 아이템은 문서에 해당되며, 평점을 relevance로 생각하면 랭킹 학습 데이터가 된다. 이는 단순한 예시며, 실제 피처를 생성하고 relevance를 정의하는 부분은 ‘정말’ 중요하고 많은 시행착오가 따른다. 지금까지 LTR 데이터셋의 형태를 알아봤다면 이제 데이터를 바탕으로 어떻게 model를 생성하고, loss를 구성하는지 살펴보겠다.

3. Learning To Rank Model Concept

이번 챕터에서는 LTR 모델 컨셉에 대해 알아보겠다. 일반적으로 LTR에서는 아래 그림처럼 relevance(score) 예측 모델을 만들게 된다. 여기서 intput은 챕터 2의 feature이며, 모델 $f(.)$는 relevance(score)를 예측한다는 측면에서 scoring function이라 한다.

Intro에서 언급했듯 앞으로 다룰 모델은 크게 3가지(RankNet, LambdaRank, LambdaMART)이다. 각 모델은 디테일한 차이들이 있지만, 컨셉 측면에서만 나눠보면 RankNet과 LambdaRank는 score 자체를 예측하는 모델이고, LambdaMART는 score의 변화량을 예측하는 모델이다. 우선 여기까지만 이해하고, 이게 무슨말인지는 아직 몰라도 되겠다. 지금 우리가 알아야 할 것은 LTR 모델은 relevance(score)를 예측하는 것이고, 이 값이 큰 순서에 따라 추천한다는 것이다.

4. Learning To Rank Loss Concept

흔히 LTR 알고리즘을 검색하면 가장 많이 나오는 내용이 Pointwise, Pairwise, Listwise이며, 이는 정확히 loss를 정의하는 방법들이다. loss는 실제값과 예측값으로 이뤄지므로, 3가지 방법의 차이는 ‘예측값’이 결정한다고 할 수 있다(실제값은 모두 동일하므로). 필자는 그냥 쉽게 ‘랭킹을 만드는 컨셉’으로 이해하고 있는데, 왜냐하면 예측값 정의에 따라 문서들의 랭킹이 결정되기 때문이다. 무슨 말인지 하나씩 살펴보자.

Pointwise

일반적으로 LTR task는 binary classification 문제로 치환해서 문제를 해결하는 경우가 많다. pointwise 경우, 아래처럼 relevance > 0 일 때 label을 1로 주어 binary 문제를 만들 수 있다.

pointwise dataset

pointwise의 핵심은 개별 아이템 별로 예측값을 생성하는 것이다. 즉 모델이 주는 score 값을 토대로, 그 아이템이 유저와 얼마나 관련이 있는지( 즉 그 아이템을 유저가 얼마나 선호하는지) 확률로 나타낸다. 이를 표현하면 아래와 같다.

\[\begin{align*} f(x_i) = s_i \ \ \ &\rightarrow \ \ \ p(I_i \ \text{is relevant}) : = p_i = \frac{1}{1+e^{-s_i}}, \ \ \ where \ i=1,2,3 \\ \\ & \therefore \ \text{Loss function}= L(y_i, p_i) \end{align*}\]

여기서 loss function은 문제에 맞게 설정하며 이를 바탕으로 모델 파라미터를 업데이트 한 후, 아이템별 최종 랭킹은 모델 score값으로 결정한다.

Pairwise

pointwise는 예측값 $p$ 생성시 하나의 아이템만 고려했다면, pairwise는 두 개의 아이템을 고려하는 것이 특징이다. 이를 위해 pointwise와는 다른 데이터가 필요하다. 아래는 아이템 pair를 생성해 relvance를 비교한 결과를 label로 생성한 것이다. 예를 들어 $I_i$의 relevance가 $I_j$ 보다 크다면 label을 1로 주는 식이다.

pairwise dataset

pairwise의 경우 두 개의 아이템을 고려하므로, score 값도 두 개가 필요하다. 이를 바탕으로 두 아이템 중 어떤 아이템이 유저와 더 관련이 있는지 확률로 나타낸다. 이를 표현하면 아래와 같다.

\[\begin{align*} f(x_i) = s_i, \ \ f(x_j) = s_j \ \ \ \rightarrow \ \ \ & p(I_i > I_j) := p_{ij} = \frac{1}{1+e^{-(s_i-s_j)}} \ \ \ where \ i,j=1,2,3 \ \ \text{and} \ \ i \ne j \\ \\ & \therefore \ \text{Loss function}= L(y_{ij}, \ p_{ij}) \end{align*}\]

예를 들어 $s_i$ 가 $s_j$ 보다 월등히 크다면 $ p(I_i > I_j)$가 1로 수렴하는 식이다. 마찬가지로 loss function은 문제에 맞게 설정하며, 모델 파라미터를 업데이트 한 후, 아이템별 최종 랭킹은 모델 score 값으로 결정한다.

중요한 점은 두 아이템 간의 ‘상대적인 우위(선호)’를 고려하여 랭킹을 생성한다는 것이다. 이는 pointwise가 개별 아이템만을 고려하는 것에 비해 훨씬 더 많은 정보를 담고있다. pairwise는 LTR에서 가장 흔히 사용되는 loss 컨셉이므로 중요한 내용이라 할 수 있다.

Listwise

pairwise가 두 개의 아이템을 고려하여 예측값을 생성했다면, listwise는 전체 아이템을 고려한다. 여기서는 ListNet 논문에 나와있는 아이디어를 간단히 살펴보겠다. listwise는 모든 아이템을 순서대로 나열(순열)해 보면서 loss가 가장 작아지는 최적의 순서를 찾는 방법이다. 예를 들어 아래와 같이 3개의 아이템이 존재할 때, 총 6가지의 순열을 생성할 수 있다.

listwise dataset

설명을 위해 몇 가지 노테이션을 정의 해보겠다.

\[\begin{align*} x &= (x_1, \ldots, x_n) \ \ where \ \ n= \text{the number of items} \\ y &= (y_1, \ldots, y_n) \\ \end{align*}\]

여기서 $x$는 feature 리스트, y는 relevance 리스트다. 우리 예시의 경우 아이템이 3개이므로 $n=3$이다. 또한 순열 $\pi$에 대한 정의는 다음과 같으며, $\pi(j)$ 는 $j$번째 위치에 오는 아이템을 가리킨다. $\Omega_n$는 모든 가능한 순열 집합으로 우리 예시의 경우 $\Omega_n =$ { $\pi_1, …, \pi_6$ } 이다.

\[\begin{align*} \pi &= <\pi(1), \ldots, \pi(j), \ldots, \pi(n)>, \ \ \pi \in \Omega_n \end{align*}\]

listwise는 아이템 전체를 고려하므로, score값도 전체를 사용하며 이를 바탕으로 순열 $\pi$에 대한 확률을 구하게 된다. 이 확률은 순열 $\pi$가 얼마나 가능성 있는 순서인지 나타내는 값 정도로 이해하면 되겠다. 또 $\phi(.)$는 맵핑함수로 논문에 따르면 strictly increasing function을 가정하며 exponential 함수를 예로 사용하고 있다.

\[\begin{align*} f(x) = (s_1, s_2, ...,s_n) := z \ \rightarrow \ \ p_z(\pi)&= \prod_{j=1}^{n} \frac{\phi(z_{\pi(j)})}{\sum_{k=j}^{n} \phi(z_{\pi(k)})} \ \ \ \ \ s.t. \sum_{\pi \in \Omega_n} p_z(\pi) =1 \\ \\ \therefore \ \ \text{Loss function} = L(y, z) &= -\sum_{\pi \in \Omega_n} p_{y}(\pi) log(p_{z}(\pi)) \end{align*}\]

여기서는 cross entropy loss function을 사용하였고, 순열 $\pi$에 대한 실제값과 예측값은 각각 $p_y(\pi)$ , $p_z(\pi)$ 이다. 이해를 돕기 위해 $\pi_5 = <\pi(1), \pi(2), \pi(3)> = < I_3, I_1, I_2>$을 예로 들어보자.

\[\begin{align*} p_y(\pi_5) &= \frac{\phi(y_{\pi(1)})}{ \phi(y_{\pi(1)}) + \phi(y_{\pi(2)}) + \phi(y_{\pi(3)}) } \times \frac{\phi(y_{\pi(2)})}{\phi(y_{\pi(2)}) + \phi(y_{\pi(3)}) } \times \frac{\phi(y_{\pi(3)})}{\phi(y_{\pi(3)}) } \\ &= \frac{\phi(y_3)}{ \phi(y_3) + \phi(y_1 ) + \phi( y_2 )} \times \frac{\phi( y_1 )}{\phi( y_1 ) + \phi( y_2 ) } \times \frac{\phi( y_2 )}{\phi( y_2) } \\ \\ \\ p_z(\pi_5) &= \frac{\phi(z_{\pi(1)})}{ \phi(z_{\pi(1)}) + \phi(z_{\pi(2)}) + \phi(z_{\pi(3)}) } \times \frac{\phi(z_{\pi(2)})}{\phi(z_{\pi(2)}) + \phi(z_{\pi(3)}) } \times \frac{\phi(z_{\pi(3)})}{\phi(z_{\pi(3)}) } \\ &= \frac{\phi(s_3)}{ \phi(s_3) + \phi(s_1 ) + \phi( s_2 )} \times \frac{\phi( s_1 )}{\phi( s_1 ) + \phi( s_2 ) } \times \frac{\phi( s_2 )}{\phi( s_2) } \\ \end{align*}\]

순열 기반 listwise는 아이템의 개수가 많아지면 계산량도 기하급수적으로 늘어나므로 실제로 사용하기가 어렵다. 따라서 논문은 첫 번째 자리만 고려해 확률을 계산하는 방식을 제안한다. 방법이 어떻든 listwise는 모든 아이템을 고려해 예측값을 생성한다는 것이 가장 중요하다. 이후에 설명할 LambdaMART 역시 listwise 컨셉을 따르기 때문에 그 때 조금 더 살펴보도록 하겠다.

5. Conclusion

이번 포스팅에서는 Learning To Rank에 대한 전반적인 내용을 살펴봤다. 모든 문제가 그렇지만, LTR은 특히 데이터를 제대로 이해하지 못하면 model이나 loss에 관한 내용을 정확하게 파악하는게 어렵기 때문에 되도록 데이터와 함게 설명해보았다. 다음 포스팅은 서두에서 말했듯이 LTR 모델 중 하나인 RankNet에 관해 살펴보도록 하겠다.

Reference

Wikipedia - Learning To Rank

TF-Ranking- ICTIR 2019