[논문 리뷰] DeepFM: A Factorization-Machine based Neural Network for CTR Prediction

Recommender System

• collaborative filtering
• click-through rate prediction
• session-based recommendation

본 논문은 다양한 추천 중, click-through rate prediction에 관한 내용을 다루고 있습니다.

Abstract

DeepFM이란 click trhough rate(CTR)을 예측하는 모델이다. 이는 Factorization-Machine(FM)과 Deep Learning(DL)을 통합한 것으로, feature들의 interaction을 모델링 하는 것이 특징이다. 기존 모델들은 low-order feature interaction 또는 high-order feature interaction 중 하나만 고려한 반면, DeepFM은 두 interaction을 모두 표현할 수 있는것이 핵심이다. 이와 비슷한 아이디어를 갖는 Wide & Deep model과 달리 DeepFM은 FM파트와 DL파트가 같은 input을 공유하며 별도의 feature engineering이 필요없다는 것이 가장 큰 차이점이다.

1. Introduction

Goal

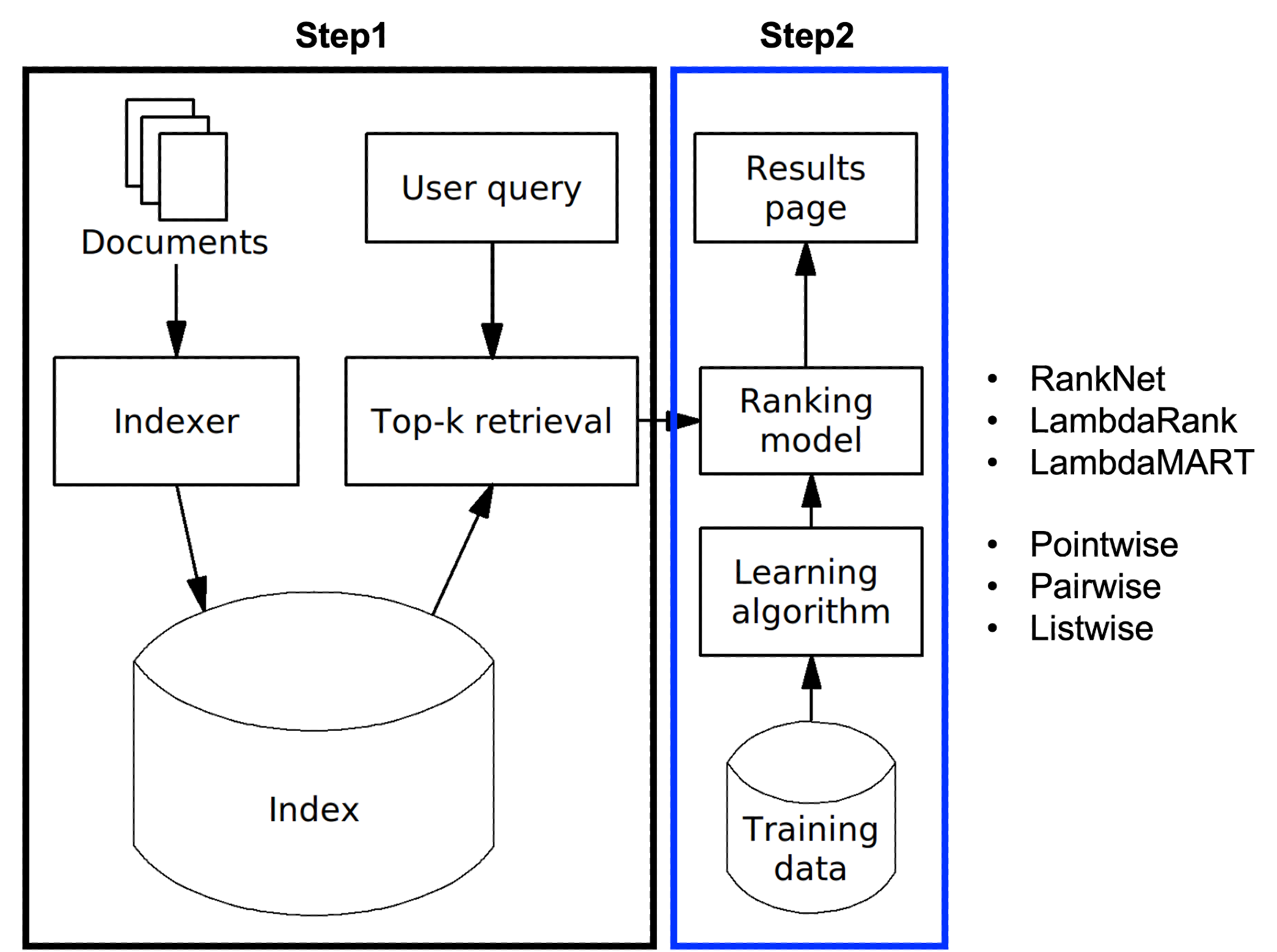
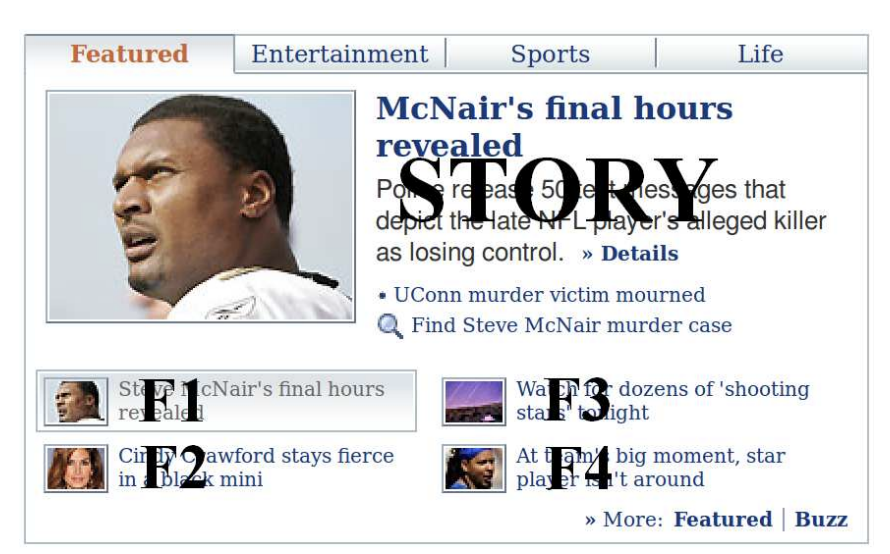
CTR 예측이란, 아래 그림처럼 user에게 추천 아이템들이 주어졌을 때 user가 해당 아이템을 클릭할 확률을 추정하는 것이다. 이때 추정된 확률을 바탕으로, user의 선호 아이템 순위를 메길 수 있다.

What is feature interaction

CTR을 정확하게 예측하기 위해서는, user의 클릭 로그로부터 feature interaction을 면밀히 파악하는 것이 중요하다. 아래는 다양한 상황으로부터 고려할 수 있는 interaction 예시다 .

• 사람들은 식사시간에 배달앱을 다운로드하는 경향이 있다.

  $\rightarrow$ ‘app category’ 와 ‘time’ 간의 interaction 존재 (order-2)

• 10대 남자들은 rpg 게임을 선호한다.

  $\rightarrow$ ‘app category’ 와 ‘gender’ 와 ‘age’ 간의 interaction 존재 (order-3)

• 사람들은 맥주와 기저귀를 함께 구매하는 경향이 있다.

  $\rightarrow$ ‘beer’ 와 ‘diaper’ 간의 숨겨진 interaction 존재 (order-2)

위의 두 예시는 발견하기 쉽고 또 이해하기도 쉬운 반면, 마지막 예시는 모델이 자동으로 찾아주지 않으면 포착하기 어려운 interaction 일 수 있다. 따라서 CTR 예측모델을 고려할 때는, 명시적인 interaction과 숨겨진 interaction을 둘 다 잡아낼 수 있는 모델을 고려하는 것이 중요하다. (DeepFM이 두 파트로 구성된 이유)

Previous studies

interaction을 고려하는 모델에는 아래와 같은 것들이 있으며, 각각 장단점이 존재한다.

• Generalized Linear Model (GLM)

  $\rightarrow$ 일반적으로 order-2 interaction까지만 고려하며 그 이상은 일반화 하기가 어렵다.

• Factorization Machine (FM)

  $\rightarrow$ low-order 뿐만 아니라 high-order interaction도 이론상으로 모델링 가능하다. 하지만 후자까지 고려할 경우 모델의 complexity가 너무 커져 사실상 사용하기 어렵다.

• Factorization Machine supported Neural Network (FNN)

  $\rightarrow$ NN 기반이므로 high-order interaction은 모델링 가능하다. 하지만 low-order를 제대로 포착하기 어렵고 pre-train FM 을 사용하기 때문에 이것의 성능이 모델 전체의 성능을 좌우하게 되는 단점이 있다.

• Wide & Deep model

  $\rightarrow$ linear 모델 (wide part) 과 Neural Net 모델(deep part) 을 통합한 모델이다. low-order와 high-order interaction을 모두 포착할 수 있지만, wide 파트의 경우 고도의 feature engineering이 필요하다는 단점이 있다.

Contribution

• DeepFM은 low-order와 high-order feature interaction을 모두 포착할 수 있다. 비슷한 구조인 Wide & Deep 모델과 다르게 end-to-end 방식으로 학습되며 별도의 feature engineering이 필요 없다.

• DeepFM은 FM 파트와 DL 파트가 input과 embedding 벡터를 공유하기 때문에 효율적인 학습이 가능하다.

2. Our Approach

아래는 DeepFM의 데이터 구조다. 총 $n$개의 데이터가 있다고 할 때, 각 row는 user와 item 정보를 담고 있는 $x$와 특정 아이템 클릭여부를 나타내는 $y$ 로 이루어져 있다.

\[\begin{align*} x & =[x_{field_{1}},x_{field_{2}},...,,x_{field_{j}},...,x_{field_{m}}]_{(1 \times d)} \\ y &\in \{0,1\} \end{align*}\]

먼저 $x$는 $m$개의 필드로 이뤄져 있으며 각 필드는 다양한 정보를 담고있다. 예를들어 user 필드에는 user의 id, 성별, 나이 등의 정보가, item 필드에는 특정 item의 구매 정보 등이 포함된다. 각 필드에는 카테고리 피처일 경우 one-hot 벡터로, 연속적인 피처일 경우 해당 값을 그대로 사용할 수 있다. 일반적으로 $x$는 굉장히 sparse 하며 고차원이다.

이어 $y$ 는 user의 특정 item에 대한 클릭여부를 나타낸다. 만약 user가 특정 item을 클릭 했을 경우 $y=1$, 클릭하지 않았을 경우 $y=0$이 된다.

위와 같은 데이터 구조를 고려할 때, DeepFM의 목표는 $x$ 가 주어졌을 때, user가 특정 item을 클릭할 확률을 예측하는 것이 되겠다.

\[\begin{align*} \hat{y} = \text{CTR_model}(x) = \text{DeepFM}(x) \end{align*} \\\]

Deep FM

DeepFM은 위와 같이 low-order feature interaction을 포착하는 FM 모델과, high-order feature interaction을 포착하는 DNN 모델로 구성된다. 두 모델의 구조는 이후 각각 살펴볼 것이기 때문에 여기서는 DeepFM의 Input과 output만 살펴보겠다.

Input

먼저 Input의 경우 주목할 만한 특징은 FM layer와 Hidden layer가 같은 embedding 벡터를 공유한다는 점이다. 이는 앞서 Wide & Deep 모델과의 차별점이라고도 설명했다.

여기서 embedding 벡터란, 아래와 같은 별도의 embedding layer를 훈련시켜 얻은 dense 벡터를 의미한다. 여기서 $m_{i}, \ i=1,2…,m$ 는 $x_{field_{i}}$의 차원으로, $\sum_{i=1}^m m_{i} = d$를 만족한다. ( $d$는 $x$의 차원)

\(\\\) 각 Neural Network은 hidden 벡터의 차원이 $k$로 모두 동일하며, 이는 sparse한 $x_{field_{i}}$를 $k$ 차원으로 압축시켜 표현하겠단 의미다. 이 과정에서 얻게 되는 가중치 행렬 $W_{i}$의 각 행이 바로 $x_{field_{i}}$의 각 성분에 해당하는 embedding 벡터가 된다. ($x_{field_{i}}$는 one-hot 벡터이기 때문에 만약 $j$번째 성분이 1이라면, $W_{i}$의 $j$번째 행이 해당 성분의 벡터가 됨)

예를 들어, $x_{field_{1}}$이 연령대 피처로 [10대, 20대, 30대] 와 같은 정보를 나타낸다고 하자 ($m_{1}=3$). 만약 어떤 user가 10대라면 $x_{field_{1}}=[1,0,0]$ 이 될 것이고, 10대에 해당하는 embedding 벡터는 $x_{field_{1}}W_{1}=v_{1}$, 즉 $W_{1}$의 첫번째 행벡터가 될 것이다. 즉 이 벡터를 일컬어 10대에 대한 정보가 압축된 embedding 벡터라고 한다.

\[W_{1} = \begin{pmatrix} w_{1,1} & w_{1,2} & \cdots & w_{1,k} \\ w_{2,1} & w_{2,2} & \cdots & w_{2,k} \\ w_{3,1} & w_{3,2} & \cdots & w_{3,k} \\ \end{pmatrix} = \begin{pmatrix} v_{1} \\ v_{2} \\ v_{3} \end{pmatrix}\]

정리하자면 위 그림의 Sparse Features 부분에서, 각 필드의 노란색 부분에 해당하는 embedding 벡터를 FM과 DNN 이 모두 사용하는 것이 특징이다.

Output

output 같은 경우는 아래 처럼 두 모델이 각각 내놓은 예측치를 더한 값을 최종 결과로 사용한다.

\[\begin{align*} \hat{y} = sigmoid(y_{FM} + y_{DNN}) \end{align*} \\\]

FM Component

그렇다면 이제 low-order feature interaction을 포착하는 FM 모델을 살펴보겠다.

\[\begin{align*} y_{FM} = <w,x> + \sum_{j_{1}=1}^{d}\sum_{j_{2}=j_{1}+1}^{d}<v_{j_{1}}, v_{j_{2}}> x_{j_{1}}x_{j_{2}} \ \ where \ \ w\in R^{d}, \ v_{i}\in R^{k} \end{align*} \\\]

FM 모델은 order-1 interaction을 포착하는 텀과, order-2 interaction을 포착하는 텀으로 나눠진다. 이 모델은 polynomial regression 모델과 동일하게 이해하면 된다. 다만 차이점은 order-2 interaction 텀의 가중치를 위에서 설명한 embedding 벡터들의 내적으로 사용한다는 것이다. 예를들어 10대와 20대 피처의 interaction 가중치는 10대, 20대에 해당하는 embedding 벡터들의 내적이 되는 것이다.

Deep Component

이어 high-order feature interaction을 포착하는 DNN 모델이다.

\[\begin{align*} a^{(0)} &= [e_{1},e_{2},...,e_{m}] \\ a^{(l+1)} &= \sigma(W^{(l)}a^{(l)}+b^{(l)}) \\ y_{DNN} &= \sigma(W^{|H|+1}a^{|H|}+b^{|H|+1}) \end{align*} \\\]

FM 모델에서는 embedding 벡터가 interaction 텀의 가중치의 역할을 했다면, DNN 모델에서는 input으로 사용된다. 즉 $e_{i}(= v), \ i=1,..,m$가 field $i$의 노란색 부분에 해당하는 embedding 벡터라 할때, 이런 벡터들을 모두 합친 $a^{(0)}$ 가 모델의 input이 되는 것이다. 나머지는 익히 알고있는 DNN의 구조와 동일하며, $H$ 개의 층을 모두 통과해 나온 $a^{H}$ 에 output의 차원을 맞춰준 후 sigmoid 함수를 통과한 값이 최종 결과가 된다.

Relationship with the other Neural Networks

위 표는 DeepFM 모델을 비슷한 NN 모델들과 비교한 것이다. 이는 위의 Previous studies의 내용을 표로 정리한 것 뿐이다. 다시 요약하자면, DeepFM는 low-order, high-order interaction이 모두 표현 가능하며, Wide & Deep 모델과 달리 별도의 feature engineering 이 필요없다. 또한 FNN는 FM을 미리 훈련시킨후 이를 DNN 가중치 초기화시 사용했다면, DeepFM은 FM을 DNN과 함께 훈련시키는 방식이므로 FM의 성능에 좌우되지 않는 장점이 있다.

3. Conclusion

DeepFM은 FM과 DNN을 함께 훈련시키는 모델이다. 이는 pre training이 필요없고 두 모델이 embedding 벡터를 서로 공유하기 때문에 별도의 feature engineering 이 필요없다는 것이 장점이었다. 또한 low, high order feature interaction을 모두 표현해낼 수 있었다. 나아가 여기서는 생략했지만 experiment 결과에 따르면, DeepFM은 AUC와 logloss면에서 여타 최신 모델들보다 뛰어난 성능을 보였고 효율성 측면에서도 우수했다.